SICM（逐次的情報量規準最小化法）の適用事例と特徴

社会的影響が大きい予測モデルでは可読性が重要となる

予測モデルは近年様々な場面で利用されるようになってきた。予測モデルとは出力の正解例と入力との関係をモデル化する方法の一般的な名称である。例えば、信用格付けの推定問題(ローンの貸し出しにおける貸し倒れの発生を予測・検知する問題)を考える場合には、個人のプロファイル・所得・ローン残高等を入力として貸し倒れの発生確率を出力とする予測モデルが使用される。よく使われる予測モデルとして、線形回帰・ロジスティック回帰・決定木・SVM(サポートベクトルマシン)・深層学習(ディープラーニング)等が挙げられる。

予測モデルを利用する際に重要な点として、予測精度とモデルの解釈とが挙げられる。近年、深層学習のような予測精度の高いモデルが広く使われている一方で、予測結果に対する解釈、特になぜその結果に到ったかの根拠がわからないためにビジネスでの活用を断念するという事例が目立つようになってきた。

例えば、金融業において信用格付けを予測するモデルを業務で使用する際には、規制などからそのモデルに対する説明が要請されることが多い。これはデフォルトリスクを最小化して融資を行う金融機関の収益を最大化することだけが目的なのではなく、融資を断るという判断の倫理的な正しさを担保することも目的としている。融資を断られた顧客は、それにより住宅購入できなかったり、教育を受けられなかったりと社会的な機会を喪失することになる。もし、融資判断の中で利用された予測モデルの中に過去の偏見や社会的差別に影響された傾向が内在していた場合、社会的な偏見や差別を再生産してしまう危険性がある。

一人の人生や企業の存続を左右するような判断に関わる予測モデルには、大きな社会的責任が伴う。このようなミッションクリティカルな予測モデルは、金融機関の融資のみならず、成績評価や大学入試、採用、人事評価や投資判断などで利用される。（表1参照）

表1: 可読性の高い予測モデルが求められる分野。人の評価に関わる為に受け手への影響が大きく、また判断の責任が重い為に予測モデルの使い手への影響も大きい。このような場合、モデルの結果を解釈・説明することと、不適切なモデルを人手で改修することを目的として、可読性の高い予測モデルを使うことが望ましい。

このような大きな責任が伴う判断に関わる予測モデルには、可読性が求められる。可読性とは予測モデルの以下の２つの性質を意味している。

1. 各入力変数(上記の例における所得やローン残高等)が出力にどの程度効いているかを定量的に評価できること
2. 入力からどのように出力が導かれるかが数式的に追えること

この定義に基づくと、深層学習やSVM(サポートベクトルマシン)等の予測モデルは可読ではなく、線形回帰、ロジスティック回帰や決定木等の予測モデルは可読である。

この定義からも分かるように、モデルの可読性が高いとは、モデルによる予測に対して何らかの解釈を人間が与えられる(モデルに解釈可能性がある)ということを意味する。また、数式を通じてモデルの構造を把握できるということは、何らかの恣意的な修正をモデルに組み込みやすいということも意味している。過去のデータから学習しただけのモデルではどうしても望ましくない差別や偏見などの傾向が含まれてしまう場合に、データ以外から得られる知識や合理的な判断に基づいて、影響範囲をコントロールしながら修正を行うということが、実務上しばしば必要とされる。

予測モデルの精度と可読性を両立させることは難しい

可読性の高い予測モデルとしてロジスティック回帰モデルや決定木のような構造が単純なモデルが利用されることが多い。しかし、構造が単純であるが故に、深層学習のような可読性の低いモデルに対して予測精度で劣ることが多い。つまり、予測モデルにおいて予測精度と可読性は基本的にはトレードオフの関係にあり両立させることが難しい。

このような問題に対応するため、可読なモデルを複数組み合わせて新たなモデルを構築することがある。例えば、図1のような構造の階層的なモデルが考えられる。この例では、決定木によって予測対象をいくつかのグループに分類し、グループごとにロジスティック回帰を適用している。全体のなかでは様々な傾向が混在するために単一のロジスティック回帰では十分な精度が得られなくても、適切にグループ分けすることでそれぞれのグループの中では精度の高いモデルを構築でき、(適切なグループ分けができれば)全体として精度が高まる。また、それぞれのグループごとに傾向を把握することができるので、人間にとっての可読性も高い。
 

図1:
階層的ロジスティック回帰モデル。決定木とロジスティック回帰モデルを組合せて作られる予測モデル。条件に対応するロジスティック回帰モデルを用いて予測が実行される。この図の例では、条件①を満たすレコードに対してはモデル1を用いて予測値が求められ、条件②かつ条件③を満たすレコードに対してはモデル2を用いて予測値が求められる。

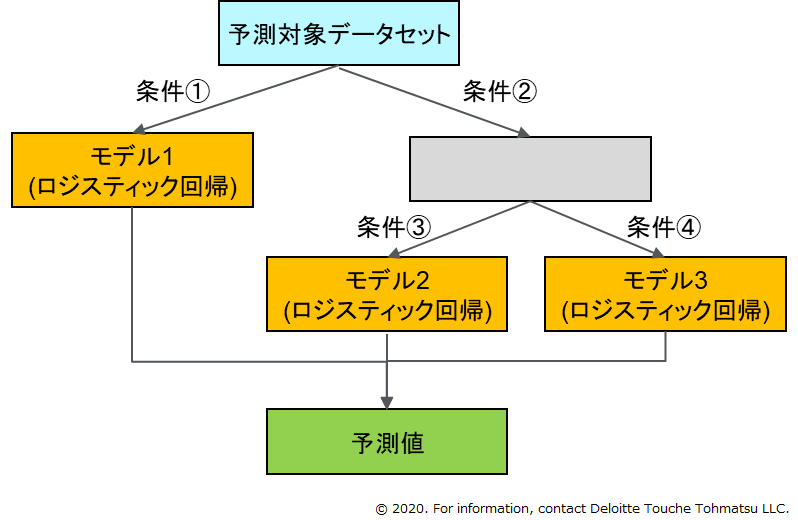
このような階層的なモデルは精度と可読性を両立しているが、「グループ分け」と「それぞれのグループの中での予測モデル」を多数作って比較するという試行錯誤を幾度も行う必要があり、大きな手間がかかっていた。

SICMアルゴリズムによって予測精度と可読性を両立するモデルを自動構築できる

上記のような背景からデロイトが独自に開発した機械学習技術がSICM (Sequential Information Criterion Minimization、逐次的情報量規準最小化)アルゴリズムである。SICMアルゴリズムを用いると、可読なモデルを組み合わせた階層的なモデルを自動的に構築できる。例えば、上記の例にSICMを適用すると「グループ分け」を行う決定木と、「それぞれのグループの中での予測モデル」であるロジスティック回帰を同時に学習し、最適な組み合わせを一度に探索することができる。

技術的な説明は後段に譲るが、SICMは特定の可読なモデルの組み合わせに特化したものではなく、様々な種類のモデル推定の為の基礎的なアルゴリズムである。情報量規準の計算と同様に、確率分布で表されるモデルであればSICMを適用できる。例えば、SICMを用いることで、線形回帰、ロジスティック回帰、混合分布、隠れマルコフモデル等のモデルの自由度を自動的に決定できる。

ここでは、SICMの応用イメージを紹介しよう。金融におけるデフォルト予測(信用格付けの推定)のために、として、図1のような階層的ロジスティック回帰モデル(条件に応じて予測するロジスティック回帰モデルを切り替える)を推定する例を説明する。

以下では、UCIレポジトリ(※1)で公開されているオープンデータ：「Default of Credit Card Clients」に対してSICMを適用して階層的ロジスティック回帰モデルを構築した例を示す。このデータセットはクレジットカード利用者がある年の10月にデフォルトしたか否かを表す二値のターゲット変数と、その月より前の半年間の履歴(請求額や支払額等)や利用者の属性(年齢や性別)等の入力変数を含むデータセットである。このデータセットを用いることで、過去の履歴と利用者の属性から、次の月にカード利用者がデフォルトするかどうかを予測するモデルを構築できる。

SICMを用いて構築したデフォルト予測モデルが以下となる：
 

図2: 
SICMを用いて構築された階層的ロジスティック回帰モデル(図1参照)におけるモデル割当ルール。分かり易くするために、決定木に含まれるルールを分解して一覧化してある。各条件の中のσは対応する入力変数の標準偏差を表す。また、「変数xがaσ以下(aσより大きい)」というのは、「変数xの値が”xの平均値+aσ”という値以下(値より大きい)」を省略したものである。各行の条件が全て満たされた場合、”モデル”列のモデルによって予測が実行される。

図3:
SICMを用いて構築された階層的ロジスティック回帰モデル(図1参照)における各ロジスティック回帰モデルの回帰係数。回帰係数が正である(対応する入力変数の値が増加するとデフォルトリスクが増加する)場合には赤で、回帰係数が負である(対応する入力変数の値が増加するとデフォルトリスクが減少する)場合には青で、回帰係数が0である(対応する入力変数がデフォルト予測に使用されない)場合には白で、枠を色付けしている。

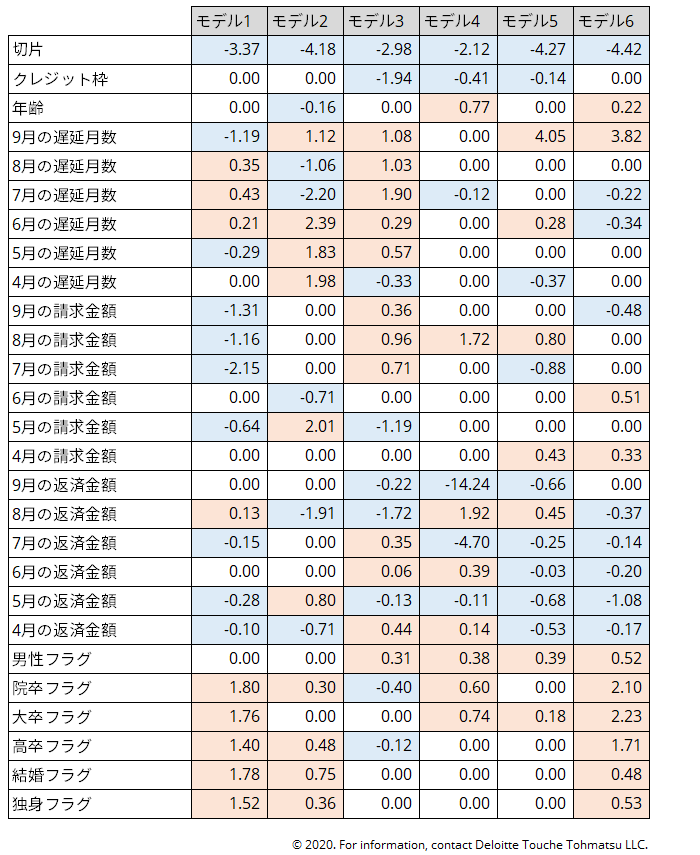
SICMを用いたモデル推定の特徴はモデル全体の構造（自由度）が自動的に決定されることである。モデル割当ルール内のグループ数は自動的に決定されているし、各ロジスティック回帰モデル内で予測に使う変数も自動的に変数選択されている(回帰係数の表で0になっている係数に対応する変数はモデルに使われなかったということ意味している)。

モデル割当ルールを見てみると、ルールによって割り振られる6個のモデルに対して以下の解釈ができる: (1)モデル1は「通常の」利用者に対応し、9月の支払い遅延が低く7月の請求額が低い; (2)モデル2は7月の請求額が通常の利用者よりも大きい利用者に対応する; (3)モデル3は通常の利用者よりも支払い遅延月数が大きい利用者に対応する; (4)モデル4、5、6は8月の支払い例外的に大きい利用者に対応する。各モデルに割り振られる利用者の数には差があり、モデル4、5、6は「例外的な」利用者を表すのに充てられている。これらの結果は以下のことを意味する:(1)通常の利用者と例外的な利用者とは別々のグループに分けてから予測する方が予測精度が向上する; (2)適切なグループ分けの仕方(通常と例外で分けるのか、年齢で分けるのか等)はSICMアルゴリズムによって自動的に決定される。

回帰係数を見ると、係数の符号がモデルに依って異なっていることが分かる。例えば、モデル2では「年齢」の係数は負であり、年齢が上がるとともにデフォルト確率が下がる。一方でモデル4, 6では係数は正であり、年齢が上がるとともにデフォルト確率が上がる。これは、8月の支払い額が例外的に大きい(>4.0σ)かどうかに依って、デフォルトリスクに対する年齢の寄与の仕方が逆になっていることを表している。このような符号の逆転を表現できる為、階層的な予測モデルは単一の予測モデルよりも高い表現力を持っており、ひいては高い予測精度を実現できる。

符号の逆転は全ての入力変数(全ての回帰係数)に対して起こるわけではない。例えば、「クレジット枠」の回帰係数はどのモデルでも常に0か正となり、信用格付けが良いほどデフォルト確率が下がる。この結果は我々の直感的な理解と合っている。

※1 UCI Machine Learning Repository: https://archive.ics.uci.edu/ml/index.php （外部サイト）

予測モデルの作成においては自由度を適切に決めることが重要となる

ここからはSICMの技術的な背景を説明する。予測モデルを構築する際には、予測精度と可読性という二つの側面から、モデルの自由度を適切に決めることが重要となる。上述の階層型モデルを例にとると、モデルの自由度とは、切り替えるロジスティック回帰モデルを何種類にするか(グループの数)や各ロジスティック回帰の中でどの変数を使うか(データセット内の入力変数の内のどれをモデルに用いるか)等のことである。

過小な自由度を持つモデルは学習データの本質的な傾向を十分には再現できない為、予測精度が低くなる傾向がある。一方で、過剰な自由度を持つモデルは学習データの本質的な傾向に加えて本来再現すべきではないノイズの性質まで再現してしまう為に、予測精度が低くなる傾向にある。従って、モデルの自由度を適切に決めることは予測精度の高い予測モデルを構築するうえで重要である。

また、全ての変数を用いたモデルよりも少数の入力変数のみを用いたモデルの方が解釈は容易になる。この為、モデルの可読性という点でも自由度を適切に決める(変数選択を実行する)ことは重要である。

自由度の異なるモデルを比較する為に情報量規準という指標がある

モデルの自由度を決定する為には、「自由度が異なる複数モデルの最適性」を定量的に比較する為の指標、つまり自由度に依存するモデルの最適性の指標、が必要となる。

そのような評価指標としてよく用いられるのが、AIC (Akaike Information Criterion、赤池情報量規準)やBIC (Bayesian Information Criterion、ベイズ情報量規準)のような情報量規準である。情報量規準は学習データへの当てはめ誤差にモデルの自由度に依存する罰則項を加えた形で表されるモデル評価指標である。

例えばロジスティック回帰モデル：

誤差項(AICとBICの表式の第一項)が確率分布を用いて表されていることからも分かるように、情報量規準は確率分布で表されるモデルに対して定義される量であり、そうでないモデルに対しては計算できない。例えば、SVM (Support Vector Machine、サポートベクトルマシン)のようなモデルに対しては情報量規準を計算できない。

自由度が異なる複数のモデルがある場合、情報量規準を最小とするモデルが最適な自由度を持つと見做すことができる。なぜならば、情報量規準には以下のような統計的によい性質がある(言い換えると罰則項の大きさがきちんとした理論から導かれている)からである。AICは期待平均対数尤度(学習データではなくテストデータに対するモデルの当てはまりの良さ≒予測精度、の評価指標の一つ)の不偏推定量(期待値が真の値と一致する推定量)である。また、BICは一致性という性質を持ち、BIC最小のモデルにおける自由度(例えばモデルに使用される入力変数の組をどのように選ぶか)は真の自由度(今の例では真の変数の組)に確率収束する。

情報量規準には統計的に良い性質を持つという利点がある一方で、最適な(情報量規準最小の)モデルを推定する為には計算時間が掛かるという困難がある。その理由は、上述の表式を見ても分かるように、情報量規準の中にパラメータ数(パラメータのL0ノルム)が含まれることにある。例えば、ロジスティック回帰モデルの場合、パラメータ数は0でない回帰係数の数となる。このような量はパラメータの値に対して連続ではない為に数値的な扱いが難しく、情報量規準を連続的に最小化するのは困難である。その為、情報量規準を用いてモデルの自由度を決定する際にはモデル比較の方法が用いられる。モデル比較の方法とは、自由度の異なる複数のモデルを構築し、それらの情報量規準を計算・比較し、その中で最も小さい情報量規準を持つモデルを採用する、という方法である。自由度の候補の数だけモデルを構築する必要がある為、モデル比較による自由度の決定には計算に時間が掛かる。

SICMアルゴリズムの技術的優位性

SICMは情報量規準を連続的に最小化する手法であり、これを用いることでモデル比較の方法を採らずにモデルの自由度を自動的に決定することが可能となる。

SICMの技術的な要点は近似計算にある。SICMでは連続な量のみで表される情報量規準の近似式を考える。近似式には連続でない量(L0ノルム)が含まれない為、連続的に最小化できる。情報量規準の代わりにこの近似式を最小化することで情報量規準を近似的に最小化しよう、というのがSICMの中心的なアイデアである。

上述の通り、自由度の決定の為に複数モデルを比較するモデル比較の方法がよく用いられる。これも上述の通り、モデル比較の方法の難点は複数モデルの構築を必要とすることによる計算コストの高さである。SICMでは単一のモデル推定で自由度を決定できる為、これらと比較すると計算コストは低い。

また、情報量規準とは別の、連続量のみで表されるモデル評価指標を連続的に最小化することでモデルの自由度を自動的に決定する手法がある。代表的な手法として、Lasso等のスパース推定が挙げられる。スパース推定では、学習データへの当てはめ誤差にモデルの自由度に依存する罰則項を加えた形で表される評価指標を連続的に最小化する。情報量規準と異なるのは、評価指標に含まれる罰則項が情報量規準ではL0ノルム(パラメータ数)に依存するのに対してスパース推定ではL1ノルム(パラメータの値の絶対値)に依存する点である。

スパース推定に対するSICMの利点は主に以下の二つである。第一に、モデル数の推定ができる。例えば、上述の階層的ロジスティック回帰モデルの場合に決定すべき自由度として、幾つのロジスティック回帰モデルを切り替え先として用意するか(モデル数の決定)、と各ロジスティック回帰モデルでどの変数を使うか(変数選択)がある。この場合に、変数選択はSICMでもスパース推定でも実行可能だが、スパース推定ではモデル数の決定が難しい。この理由は、罰則項としてモデル数(L0ノルム、SICMの罰則項)を使うのは容易だが、それに対応するスパース推定の罰則項(L1ノルム、何らかの絶対値)をどのように導けばよいかが自明ではないからである。第二に、評価関数の形が自然である。SICMでは評価関数として情報量規準を用いるが、これらは上述の通り統計的によい性質を持つことが知られている。一方で、スパース推定で用いられる評価関数は、形は情報量規準と似ているがそのような性質を持つことは示されていない。

まとめ

デロイト トーマツ独自の機械学習技術であるSICMアルゴリズムを紹介した。SICMは確率モデルの自由度を自動的に決定する為のアルゴリズムであり、モデル評価指標の一つである情報量規準を連続的に最小化する手法である。自由度の自動決定は可読かつ高精度な予測モデルを構築するのに不可欠な技術である。本稿では、SICMを用いて構築できる可読かつ高精度な予測モデルの例として階層的ロジスティック回帰モデルを取り上げ、結果の解釈の例を示した。

可読な予測モデルを構築することやその為の方法は、近年「Explainable AI」(説明可能、解釈可能な人工知能技術)という文脈で大いに注目されている。機械学習・人工知能といった技術を使ってある種自動的な分析を実行する場合でも、その分析結果を用いて最終的な決断を下すのは人間であることが多い。そのような場合に、判断根拠なしに責任を伴う重要な決定をすることは難しい。その為、分析技術をビジネスに適用する様々な場面において、解釈可能な技術に対する需要が発生する。

本稿で紹介した自由度を自動的に決定しつつ可読な予測モデルを構築するというやり方は、Explainable AIに対する技術的なアプローチの一つであり、分析結果の適用に判断根拠が必要とされる様々な場面で用いることができる有用な方法である。

ここで説明したSICMアルゴリズムについては論文としてまとめられたもの(※2)があるので、技術的な詳細やここで割愛した例等に関してはそちらを参照して頂ければ幸いである。

※2 Hirose, S., Kozu, T., Jin, Y. et al. Hierarchical Relevance Determination based on Information Criterion Minimization. SN COMPUT. SCI. 1, 224 (2020). https://doi.org/10.1007/s42979-020-00239-3 （外部サイト）